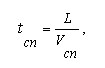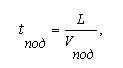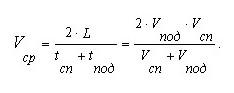|
Один тактический приём Глядя на ставшие теперь столь многочисленными телетрансляции соревнований профессионалов, всегда недоумевал: почему они уходят в отрыв преимущественно на подъёме? Это приём психологический, или за этим стоит некий физический фактор? По мере того как анализировал ситуацию, всё становилось понятным. Вслед за анализом перешёл к изменению своего собственного поведения на маршруте, так как сделанные выводы касаются не только гонщиков, но и всех нас с вами. Предлагаемый здесь анализ носит предельно упрощённый характер и учитывает только основные черты вопроса. Я совершенно не касаюсь командной тактики, игровых моментов гонки, подвергая анализу только физику явления. Первое, что приходит к каждому, едущему на длинную дистанцию - понимание того, что не важно какую мгновенную скорость ты можешь развить на коротком участке, а важно насколько велика твоя средняя скорость. Именно она определяет, в конечном итоге, время прохождения всего маршрута. А значит, если ты можешь повысить среднюю скорость, то завершишь маршрут за меньшее время, или получишь больше шансов выиграть гонку. Именно в этом состоит для спортсмена искусство правильно распределять свои силы на дистанции, так чтобы при большей средней скорости твой запас сил был больше, чем у соперника. Как это делать по отношению к подъёмам и спускам, мы разберём в этой статье. Итак разобьём маршрут на череду подъёмов и спусков, и подвергнем анализу простейший из них.
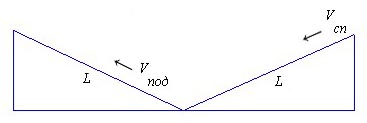
Будем считать что параметры спуска и подъёма - протяжённость, уклон - одинаковы, и подъём следует сразу же за спуском. Тогда время, затрачиваемое на спуск и подъём, рассчитывается из элементарных соотношений
а средняя скорость будет
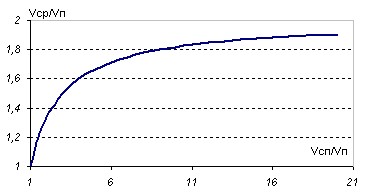
Будем считать теперь скорость подъёма неизменной, и оценим как влияет изменение скорости спуска на среднюю. Для удобства график построим в относительных единицах, т.е. обе скорости выразим в единицах скорости подъёма.
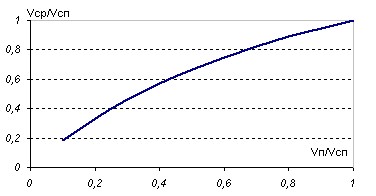
Из графика немедленно следует вывод. Как ни увеличивай скорость спуска, хоть сделай её бесконечной, средняя скорость никогда не превысит удвоенной скорости подъёма. Проанализируем теперь, как влияют изменения скорости подъёма на среднюю. График построим в долях скорости спуска, которая теперь считается неизменной.
Т.е. при увеличении скорости подъёма средняя скорость достигает значения скорости спуска в тот же момент, что и скорость подъёма. Этот случай характерен для незначительных уклонов, предыдущий - для случая подъём-спуск или спуск-подъём без учёта наката (при мгновенном изменении скорости подъёма на скорость спуска и наоборот). Так ведёт себя средняя скорость при предельных значениях скоростей подъёма и спуска. Предположим теперь, что у вас имеется некоторый запас сил и вы хотите определиться, куда его выгодней вложить: в увеличение скорости спуска или подъёма? Будем считать, что обе скорости могут быть изменены на одинаковую величину, причём, если одна из скоростей меняется, вторая остаётся неизменной. Для определения приращения средней скорости, разложим соотношение (1) в ряд Тейлора в окрестности средней скорости при исходных значениях скорости спуска и подъёма, соответственно
Пренебрегая членами разложения выше первого порядка, для приращений средней скорости получим
Введём теперь коэффициент эффективности, характеризующий соотношение приращений средней скорости
который после вычисления соответствующих производных, оказывается равным
Отсюда немедленно следует вывод. 1. Эффективность вложения резерва в увеличение скорости на подъёме всегда выше, чем в увеличение скорости на спуске. 2. При типичном двукратном превышении скорости спуска над скоростью подъёма, эффективность вложения резерва в увеличения скорости подъёма в ЧЕТЫРЕ раза выше, чем в увеличение скорости спуска. Если учесть, что энергозатраты на увеличение скорости тем выше, чем выше сама скорость, эффект станет ещё более разительным. Я анализировал также влияние более тонких эффектов на сделанные выводы. В частности, влияние наката при преодолении подъёма несколько снижает коэффициент эффективности и делает его зависимым от уклона подъёма; влияние ограничения мгновенной мощности, развиваемой велосипедистом, приводит к зависимости коэффициента не только от соотношения скоростей спуска-подъёма, но и от их абсолютных значений. Но никогда коэффициент эффективности не становится меньше предельного значения
В принципе задачу можно решать и в более сложной постановке. Например, можно искать оптимальное распределение скоростей на отдельных участках маршрута (для конкретного велосипедиста и рельефа, конечно), обеспечивающее наивысшую среднюю скорость на всём маршруте. Можно решать задачу в реальном времени, в зависимости от обстановки в гонке. Всё это интересно для спортсмена, но и туристу не помешает. Делайте выводы. Желаю успехов. ОН
P.S. А вот Том Боонен для себя уже всё решил. Цитирую комментарий Web-Еженедельника Велосипедизм 113b к 89-й Кругосветке Фландрии, состоявшейся в воскресенье 3 апреля 2005 г: "Гонка развивалась своей собственной жизнью и ближе к концу определились ее несомненные лидеры. Таких оказалось несколько: немец Андреас Клир (второе место), немец Эрик Цабель (четвертое место), Петер ван Петегем (третье место), а также итальянец Баллан. Среди них не было Тома Боонена. Вернее он был, появлялся периодически и опять отходил во вторую группу отрыва. Так было до знаменитой "Стены" у Geraardsbergen с ее 20-ти процентным подъемом. У начала стены его не было. Но когда лидеры начали яростно карабкаться вверх по брусчатке, то к своему удивлению комментаторы, увлеченные обсуждением эпизода, вдруг с изумлением обнаружили среди лидеров и Боонена! Откуда он взялся? Но факт остается фактом: Том сумел одной яростной короткой атакой достать лидирующую группу, оставив позади других спортсменов. Оставалось 17 километров до финиша".
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||