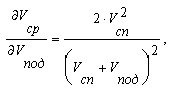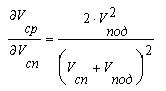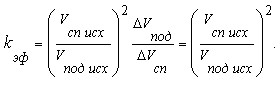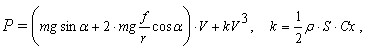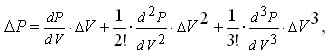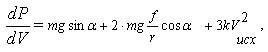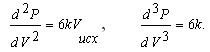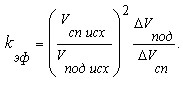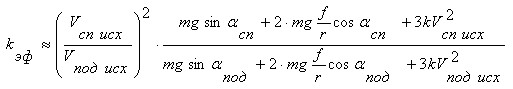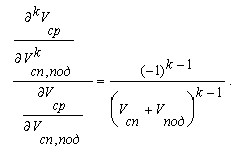|
Один тактический приём Необходимое предисловие Статья с этим названием, написанная в апреле 2005г и размещённая в Еженедельнике Велосипедизм №114b, совершенно неожиданно для меня оказалась весьма дискуссионной, а высказанные в ней взгляды получили прямо противоположные оценки - от безоговорочной поддержки до резкого неприятия. Прошедшая с 20 по 22 января 2006г на Велозоне WWWBoard конференция "Один тактический приём, или о пользе подъемов" расставила многие точки над i, в значительной степени примирила полярные точки зрения, уточнила многие оценки, выявила неточности. Хочу поблагодарить всех принявших в ней участие - а это более 300 человек - за непредвзятое отношение и неподдельный интерес к проблеме. В предлагаемой новой редакции я постарался учесть непосредственно касающиеся изложения мнения, внести необходимые дополнения и исправления. Прежняя редакция сохранена в неизменном виде во-первых для истории, а во-вторых из неизменной любви автора к размещённому в ней "поэтическому" творению. Основные результаты прежней редакции Глядя на ставшие теперь столь многочисленными телетрансляции соревнований профессионалов, всегда недоумевал: почему они уходят в отрыв преимущественно на подъёме? Это приём психологический, или за этим стоит некий физический фактор? По мере того как анализировал ситуацию, всё становилось понятным. Вслед за анализом перешёл к изменению своего собственного поведения на маршруте, так как сделанные выводы касаются не только гонщиков, но и всех нас с вами. Предлагаемый здесь анализ носит предельно упрощённый характер и учитывает только основные черты вопроса. Я совершенно не касаюсь командной тактики, психологических и игровых аспектов гонки, подвергая анализу только физику явления. Первое, что приходит к каждому, едущему на длинную дистанцию - понимание того, что не столь важно, какую мгновенную скорость ты можешь развить на коротком участке, а важно насколько велика твоя средняя скорость на протяжении всего пути. Именно она определяет, в конечном итоге, время прохождения маршрута. А значит, если ты сможешь повысить среднюю скорость, то завершишь маршрут за меньшее время, или получишь больше шансов выиграть гонку. В значительной степени именно в этом состоит для спортсмена искусство правильно распределять свои силы на дистанции, решить как распорядиться запасом сил, чтобы, проехав равное с соперником расстояние, оказаться ближе к финишу. Как это сделать по отношению к подъёмам и спускам, мы разберём в этой статье. Итак, разобьём маршрут на череду подъёмов и спусков и подвергнем анализу простейший из них.
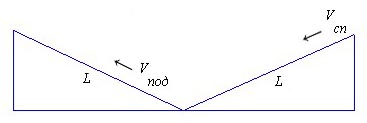
Будем считать, что параметры спуска и подъёма - качество дорожного покрытия, протяжённость, уклон - одинаковы, подъём следует сразу же за спуском; что накат отсутствует, т.е. скорость при переходе от спуска к подъёму меняется мгновенно и скачкообразно. Тогда время, затрачиваемое на спуск и подъём, рассчитывается из элементарных соотношений
а средняя скорость будет
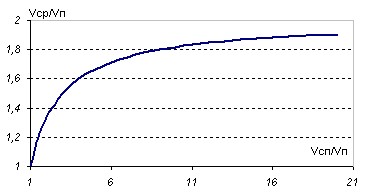
Будем считать теперь скорость подъёма неизменной и оценим, как влияет изменение скорости спуска на среднюю. Для удобства график построим в относительных единицах, т.е. обе скорости выразим в единицах скорости подъёма.
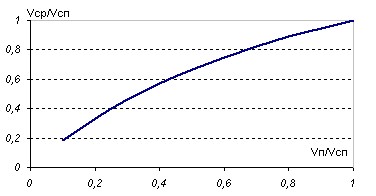
Из графика немедленно следует вывод. Как ни увеличивай скорость спуска, хоть сделай её бесконечной, средняя скорость никогда не превысит удвоенной скорости подъёма. Проанализируем теперь, как влияет изменение скорости подъёма на среднюю. График построим в долях скорости спуска, которая теперь считается неизменной.
Т.е. при увеличении скорости подъёма средняя скорость достигает значения скорости спуска в тот же момент, что и скорость подъёма. Физически последний случай реализуется при незначительных уклонах, предыдущий - для случая подъём-спуск или спуск-подъём без наката. Как справедливо отметил участник WWWBoard конференции Е.И. (прошу прощения за Nickname), соотношение (1) симметрично относительно замены скорости спуска на скорость подъёма. Непосредственное следствие этого: обе кривые - суть части единого целого. Нижняя реализуется при скорости подъёма меньшей скорости спуска - слева и ниже точки (1,1) на графиках, верхняя - продолжение нижней кривой на правую верхнюю по отношению к точке (1,1) область. При переходе через точку (1,1) скорость подъёма переходит в скорость спуска и наоборот. Так ведёт себя средняя скорость при предельных значениях скоростей спуска и подъёма. Предположим теперь, что у нас имеется некоторый запас сил и мы хотим определиться, куда его выгодней вложить: в увеличение скорости спуска или подъёма? Будем считать, что обе скорости могут быть изменены на одинаковую величину, причём если одна из скоростей меняется, вторая остаётся неизменной. Для определения приращения средней скорости разложим соотношение (1) в ряд Тейлора в окрестности средней скорости при исходных значениях скорости спуска и подъёма, соответственно
Здесь и далее производные вычисляются при исходных значениях скоростей спуска и подъёма. Пренебрегая членами разложения выше первого порядка, для приращений средней скорости получим
Введём теперь коэффициент эффективности, характеризующий соотношение приращений средней скорости
который после вычисления соответствующих производных
и подстановки в них исходных значений скоростей спуска и подъёма, оказывается равным
Отсюда немедленно следует вывод. 1. Эффективность вложения резерва в увеличение скорости на подъёме всегда выше, чем в увеличение скорости на спуске. 2. При двукратном, к примеру, превышении скорости спуска над скоростью подъёма, эффективность вложения резерва в увеличения скорости подъёма в ЧЕТЫРЕ раза выше, чем в увеличение скорости спуска. Если учесть, что энергозатраты на увеличение скорости тем выше, чем выше сама скорость, эффект станет ещё более разительным. Таковы были основные результаты статьи в прежней редакции. Новые результаты Как это ни смешно, но по-видимому именно квадратичный характер зависимости введенного коэффициента эффективности от соотношения скоростей вызвал несогласие и стремление оспорить результаты. Слишком уж неравноценными оказались спуск и подъём. Попытки найти ошибки в преобразованиях не изменили результатов, что заставило подвергнуть сомнению обоснованность принятых допущений. Главное из них - допущение о равенстве приращений скоростей спуска и подъёма, приведенное в работе без каких-либо обоснований, вызвало впечатление математического курьёза, не имеющего под собой ни необходимости, ни реальной почвы. Вместе с тем необходимость введения какого угодно допущения, уравнивающего изменения на спуске и подъёме, совершенно очевидна. В качестве него с одинаковым успехом могут выступать: - равенство приращений скоростей спуска и подъёма; - равенство приращений мощности, развиваемой велосипедистом на спуске и подъёме; - равенство развиваемых усилий в начальный момент времени и их приращений, например, вращательного момента на оси каретки или тягового усилия, приложенного к центру масс системы велосипед-велосипедист и т.п. Только это допущение позволяет обоснованно оценить, где разным гонщикам лучше отдавать свои силы – на спуске или на подъёме. Если от него вообще отказаться, то сравнивать между собой будет нечего, ведь получаемый результат будет вызван разными вложениями. Всем известно, что на спуске крутить педали легче, а едешь быстрее. Из этого совершенно необоснованно складывается убеждение, что на спуске и приращения скорости равного с приращением на подъёме можно достичь меньшими усилиями. На самом деле это совсем не так, об этом уже говорилось в прежнем варианте статьи. Численный расчёт, выполненный с учётом силы трения качения и сопротивления воздуха, подтверждает последнее. Привожу результаты расчёта приращений мощности на спуске и подъёме при условии одинаковой начальной мощности развиваемой велосипедистом, полученные GDT и Paralizёr'ом (Nickname'ы Велозоны) с использованием Калькулятора (параметры велосипедиста - по умолчанию, велосипед - MTB):
Примечание. Положительные уклоны - подъёмы, отрицательные - спуски. Приращения мощности ведут себя закономерно: на спуске растут пропорционально скорости и величине уклона, на подъёме растут пропорционально величине уклона (скорость при этом падает). Вычисляя и анализируя разности приращений мощности, несложно заметить, что одинаковое приращение скорости спуска или подъёма требует больших приращений мощности на спуске, чем на подъёме. И хотя причины этого различны - на спуске преобладает аэродинамическое сопротивление, на подъёме скатывающая сила - это означает, что попытка увеличить мощность на спуске на одинаковую величину с приращением мощности на подъёме приведёт к меньшему приросту скорости, а значит коэффициент эффективности возрастёт ещё больше. Для тех, кого численные расчёты не убеждают, привожу доказательство последнего утверждения в общем виде. В соответствии с работой В.П.Любовицкого Гоночные велосипеды.- Л.:Машиностроение,1989, мощность P развиваемая велосипедистом равна где
m - масса велосипеда и велосипедиста, g=9,81
- ускорение свободного падения, f -
коэффициент трения качения колеса, r -
радиус колеса, Раскладывая выражение для Р в окрестности Рисх в ряд Тейлора и выражая приращение мощности ΔP как функцию приращения скорости ΔV, получаем где производные вычисляются при исходном значении скорости и имеют вид
Выражение для ΔP имеет только три первых производных, так как все остальные производные равны нулю. Вычисляя ΔPсп и ΔPпод и их разность при одинаковых приращениях скорости на спуске и подъёме, получаем для разности приращений мощности выражение
которое положительно для всех уклонов и равно нулю на равнине. Единственное отрицательное слагаемое - разность синусов - совершенно подавляется вторым слагаемым в квадратных скобках. Последнее проверялось численно, варьируя мощность, уклон и параметры велосипедиста в разумных пределах. В результате вывод: при одинаковой исходной мощности приращение мощности на спуске - ΔPсп, обеспечивающее равное приращение скорости с приращением скорости на подъёме, всегда больше ΔPпод. Верно и обратное: одинаковое вложение мощности всегда обеспечивает больший прирост скорости на подъёме, чем на спуске, т.е ΔVпод/ΔVсп всегда больше 1 и коэффициент эффективности, имеющий в этом случае вид
ещё больше возрастает. Последняя формула - приближённая, дающая значение коэффициента эффективности примерно с 5% погрешностью, точная формула слишком сложна. Для полноты и завершённости выполненного анализа желательно получить ответ на вопросы: - достаточно ли учитывать только первый член разложения средней скорости в ряде Тейлора или добавление последующих членов может изменить результат? - не лучше ли работать в относительных единицах - относительных приращениях скоростей спуска и подъёма? Уже простой численный расчёт по точной формуле (1) убеждает в обратном: результаты совпадают вплоть до 7-и и более значащих цифр после запятой. В точной же постановке ответ лежит в соотношении членов разложения выше первого к первому (нумерация членов ряда начинается с нулевого). Привожу без вывода общую формулу для этого отношения
Естественно, берутся одноимённые индексы у скорости в числителе и знаменателе, k здесь - номер производной. Наличие в знаменателе суммы (Vсп+Vпод) в степени к-1 говорит о полном отсутствии необходимости учёта последующих членов разложения. Строгие доказательства утверждений этого раздела вынесены за пределы статьи, чтобы частоколом формул не заслонить основной смысл. Любителям последних сюда. Обсуждение результатов Конечно есть ещё множество эффектов, оказывающих влияние на коэффициент эффективности - биомеханический КПД гонщика, КПД цепной передачи, учёт влияния упругих деформаций рамы и спиц и т.д. Однако мне кажется, что основные эффекты уже нашли своё отражение в изложенном, а более точные постановки найдут своего пытливого исследователя. Полностью со всеми материалами WWWBoard конференции можно ознакомиться здесь. Конечно, при патологическом стремлении оспорить результаты можно и далее высказывать различные мнения, но вряд ли они будут сколько-нибудь обоснованными. А необоснованные утверждения навряд ли добавят чести высказывающемуся. Для того чтобы оценить сполна величину эффекта от разумного вложения сил, привожу небольшую табличку численных значений коэффициента эффективности
Да, вот именно во столько раз! Однако цифры настолько впечатляющие, что возникает справедливый вопрос: "Если эффект настолько велик, то неужели о нём никто не знает и никто не пользуется?" Да нет же, именно знают и пользуются. Знают все спортсмены и все тренеры - огромные хранилища эмпирических знаний и опыта, полученных в результате проб и ошибок. Реальную ситуацию исчерпывающе объясняет подсчёт энерготрат на прохождение последовательности спуск-подъём, например, с 10%-ми уклонами, общей протяжённостью 10 км (т.е. по 5 км на каждый).
В первом случае мощность
распределена поровну между спуском и
подъёмом; во втором гонщик на спуске не
крутит, а весь выигрыш мощности
переброшен со спуска на подъём; в
третьем на спуске по-прежнему не крутит,
а на подъёме мощность вблизи "красной"
зоны. В
результате. 1. Коэффициенты
эффективности сближаются, падают по
величине и при равенстве скоростей
сравниваются с 1. Необходимое заключение В заключение хочу предостеречь читателя от излишне прямолинейного восприятия изложенного и сведения сказанного к рекомендациям типа: "На подъёме - крути, на спуске - спи". Стремление свести всё многообразие возможных ситуаций к узкому набору железобетонных правил ещё никогда не приводило к успеху. Достаточно вспомнить о забитых на подъёмах ногах или о том, что качество покрытия на подъёме может оказаться хуже, чем на спуске ... Хотелось бы также, чтобы у вас не сложилось впечатление, что всё известно, всё открыто и делать в этой сфере нечего. Такие как Эдди рождаются раз в столетие, а результаты неуклонно растут. Значит, есть резервы, есть порох в пороховницах и место для приложения своих сил и своего интеллекта. Наконец, последнее: нужен ли был проведённый анализ? Для спортсменов нет, у них мы, скорее всего, учимся, поверяя их действия алгеброй. А вот для обычных людей, велотуристов и просто любителей, для тех, за которыми не едут машины сопровождения или хотя бы тренер на мопеде, безусловно нужен! Им приходится доходить до всего своим умом. И всё сказанное необходимо, чтобы пересмотреть свои интуитивные представления, понять, как нужно и почему. Чтобы осознать, что поведение гонщиков на этапе отнюдь не случайно, а глубоко закономерно и вполне поддаётся анализу. Например, находит своё простое объяснение другая типичная ситуация в гонке: после крутого поворота нужно готовиться к рывку пелотона, заранее наращивая передачу. Рывок после поворота - вовсе не блажь впереди идущих. Просто в крутом повороте объективно падает скорость, и чем быстрее её нарастишь до прежней, тем меньшими будут потери средней скорости. Таким же, скорее всего, должно быть и отношение к ветру попутному и встречному в классическом критериуме, например. Да и круговое педалирование проистекает, по-видимому, из того же источника - поменьше вариаций скорости, какой угодно: скорости вращения педалей, мгновенной скорости движения и т.д. Причём уменьшать вариации нужно поднимая скорость до средней на тех участках, где она объективно падает. Поднимать, разумно перераспределяя силы. Делайте выводы. Желаю успехов. ОН Благодарности. Хочу поблагодарить GDT, Е.И., On и Paralizёr'а за теплоту и дружественность общения, чёткую обоснованность и аргументированность позиции. Отдельно хочу поблагодарить мою жену за терпеливое отношение к моему сидению за компьютером и поддержку.
P.S. В прошлый раз я заканчивал статью выдержкой из комментариев к финишному рывку Тома Боонена на Туре Фландрии. На этот раз предлагаю вам отрывок из книги Лэнса Армстронга "Не только о велоспорте. Моё возвращение к жизни": "... На протяжении всей гонки я выжидал, выжидал, выжидал. Я сдерживал себя, как просил меня Оч. Последние 14 кругов до финиша я держался в лидирующей группе - и там же был Индурайн, великий испанец. Наконец на предпоследнем подъёме я пошел в отрыв. Когда я достиг перевала, вся остальная группа висела у меня на хвосте. Я скатился вниз и с лету стал подниматься на крутой склон, называемый Экеберг. Остальные следовали по пятам. Тогда я сказал себе: "Сейчас или никогда" - и, встав на педали, начал новую атаку. На этот раз между мной и остальными образовалась брешь. По другой стороне Экеберга тянулся длинный и опасный спуск. Протяженность его составляла четыре километра, и на мокрой дороге случиться могло все что угодно. Но все повороты я прошел четко, ни разу не поскользнувшись, и уже в самом низу оглянулся, чтобы посмотреть, кто следует за мной. Не было никого ..." И помните, у каждого в жизни есть свой подъём! Не пропустите его! ОН
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
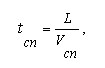
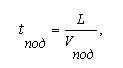
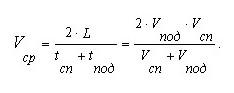
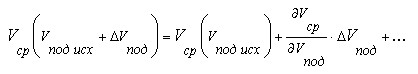 ,
,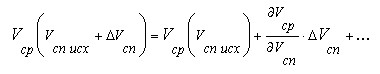 .
.
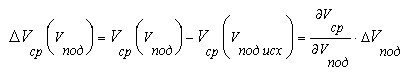 ,
,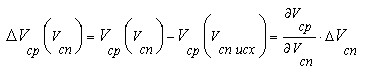 .
.
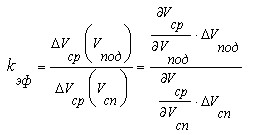 ,
,